Поэтому используя аналогию математических методов исследования спектральных характеристик пространственных и временных сигналов, распределение комплексных амплитуд спектра пропускания в дифракционном изображении пространственной квазипериодической струк-туры ЛЗ, можно определить как , или с уче-том (2.5) .

Полученное выражение описывает амплитудный спектр функции пропускания квазипериодической пространственной структуры ЛЗ. Энерге-тический спектр этой функции может быть определен с помощью теоремы Хилли [3.11] как , или же

.

Однако в работах [16, 17] показано, что для квазипериодического сигнала, описываемого единично-нулевой функцией вида (2.4)

(2.8), где - дискретная составляющая спектра на нулевой частоте, которая для квазипериодической структуры ЛЗ будет равна

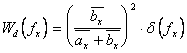(2.9) , а - непрерывная составляющая спектра, равная: 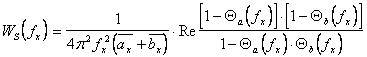(2.10), что справедливо для и не равных 1, согласно [3.35].

В выражениях (2.9) и (2.10) параметр является пространственной частотой энергетического спектра исследуемого сигнала, величина которой определяется коэфициентом масштаба и зависит от схемы построения и геометрических размеров оптической системы КОС.

Для определения формы энергетического спектра пространственной структуры ЛЗ рассмотрим вещественную часть комплексной дроби в выражении (2.10), обозначив ее через В, т.е.

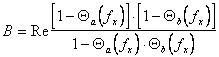(2.11). Подставив в (2.11) выражения (2.6) и (2.7) характеристических функций и получим:

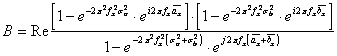(2.12).

Выражение (2.12) представляет собой комплексную дробь вида , вещественная часть которой равна (2.13).

Тогда, выполнив алгебраические преобразования над (2.12) с использо-ванием (2.13), вещественную часть В выражения (2.12) можно представить в виде :

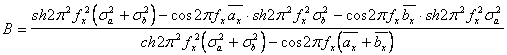(2.14).

Подставив (2.14) в (2.10), получим уравнение непрерывной составляю-щей энергетического спектра квазипериодической пространственной струк-туры ЛЗ: