Как _ видим, дополнительное слагае­мое R(rc , h, f0) в уравнении (6) зависит не только от геометрии пласта, но и от параметра Фурье (f0). В дальнейшем бу­дем называть это слагаемое функцией фильтрационного сопротивления. Заме­тим, что при h=l (скважина совершен­ная по степени вскрытия) уравнение (2) представляет собой интегрально-по­казательную функцию

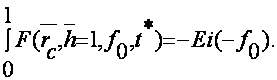(7)

С учетом равенства (7) решение (6) за­пишем в виде

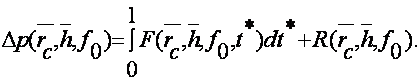(8)

Разрешая уравнение (8) относительно функции сопротивления и учитывая уравнение (2), находим

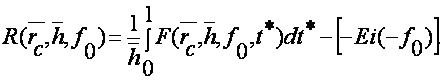(9)

и на основании равенства (7) приведем выражение (9) к виду

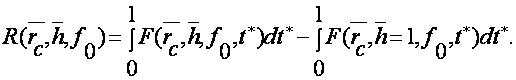(10)

Численное значение R(rс,h,fo) рас­считано по уравнению (10) на ЭВМ в широком диапазоне изменения парамет­ров rc, h, f0. Интеграл (2) вычислялся методом Гаусса, оценка его сходимости выполнена согласно работе [3]. С уче­том равенства (7) вычисления дополнительно проконтролированы по значени­ям интегрально-показательной функции.

С целью выяснения поведения депрессии и функции сопротивления проана­лизируем их зависимость от значений безразмерных параметров.

1. Определим поведение Dр в зави­симости от значений параметров rс, h, f0.

Результаты расчетов значений де­прессии для каждого фиксированного rc сведены в таблицы, каждая из кото­рых представляет собой матрицу разме­ром 10х15. Элементы матрицы это зна­чения депрессии Dp(rc) для фиксиро­ванных h и f0. Матрица построена та­ким образом, что каждый ее столбец есть численное значение депрессии в зависимости от h, .а каждая строка со­ответствует численному значению де­прессии в зависимости от fo (табл. 1). Таким образом, осуществлен переход от значений безразмерной депрессии Dp(rc, h, f0) к относительной депрессии

Dр*i,j (rc).

Для удобства построения и иллюст­рации графических зависимостей выпол­нена нормировка матрицы. С этой це­лью каждый элемент i-й строки матри­цы поделен на максимальное значение депрессии в данной строке, что соответ­ствует значению j==15. Тогда элементы новой матрицы определятся выраже­нием

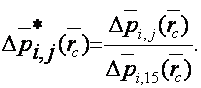(11)

Условимся элементы матрицы назы­вать значениями относительной депрес­сии. На рис. 1 приведен график изме­нения относительной депрессии при фик­сированных значениях h. Характер по­ведения относительной депрессии поз­воляет описать графики уравнением пучка прямых

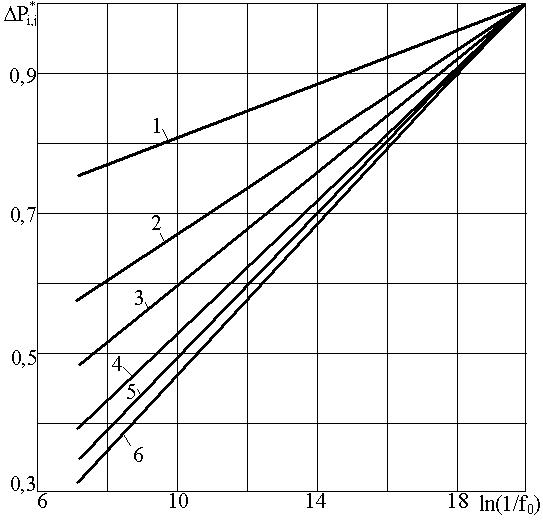Рис. 1. Поведение относительной депрес­сии (rc=0,0200, hi=const, f0) при значениях h, равных: 1— 0,1; 2 — 0,3; 3—0,5; 4 — 0.7; 5 —0,9; 6—1,0.

где ki — угловой коэффициент прямой, который определяется h и от индекса j не зависит.

Анализ зависимости поведения де­прессии Dp*i,j от f0 для всех rc >0,01 показывает, что графики этой зависимости можно описать уравнением пучка прямых для любого значения h. Для rc< 0,01 в графиках зависимости появляются начальные нелинейные уча­стки, переходящие при дальнейшем уменьшении параметра f0 (или же при увеличении его обратной величины 1/foj) в прямые для всех значений h<l,0

(рис. 2). При h=l,0 поведение депрес­сии строго линейно. Кроме того, протя­женность нелинейного участка для раз­ных rc при h=const различна. И чем меньше значение безразмерного ради­уса rc , тем больше протяженность не­линейного участка (рис. 2).