Кремний, полученный с использованием *геттерирования* расплаваСтраница 2
Физическая модель процесса
внутреннего геттерированияв кремниевой
технологии .
Как известно, металлические примеси Au, Fe, Ni, Си и другие приводят к возникновению генерационно-рекомбинационных центров в активных областях приборов на основе кремния, что в свою очередь вызывает деградацию свойств приборов. Совокупность технологических приемов, позволяющих снизить концентрацию таких центров, локализуя их вблизи преципитатов Si0x (xw2), расположенных вдали от активных областей приборов, называется методом внутреннего геттерирования (ВГ)
По технологии ВГ накоплен обширный фактический материал, однако физические принципы его механизма в настоящее время окончательно не установлены [1, 2). Широкое распространение, например, получили представления о том, что центрами геттерирования являются дислокации и дефекты упаковки, возникающие вследствие релаксации упругих полей и пересыщения по межузельному кремнию в процессе преципитации кислорода при Г>700°С. Однако эти представления не являются универсальными, что было доказано рядом исследований. Так, в работе [3) показано, что в ряде случаев эффект геттерирования проявляется и в отсутствие дислокаций и дефектов упаковки, при этом сам кислородный преципитат является геттером. Другие авторы [41 обнаружили гексагональные и ромбические дислокационные петли в отсутствие кислородных преципитатов, на основании чего сделано предположение о том, что дислокационные петли возникают при высокотемпературном отжиге вследствие растворения преципитатов, образовавшихся ранее во. время низкотемпературного отжига.
В данной работе представлены результаты исследований физических закономерностей процесса ВГ, выполненных на кафедре общей физики МИЭТ, в которых развита модель дальнодействующего механизма взаимодействия примесь-центр геттерирования. Рассмотрена модель комплекса примесь-точечный дефект, рассчитаны параметры таких комплексов и найдено их неоднородное распределение в упругом поле преципитата. Представлена также диффузионная модель ВГ на основе взаимодействия дипольных комплексов с кислородным преципитатом.
Комплексы примесь-точечный дефект и их неоднородное распределение вблизи центра гетгерировання
Принципиальное отличие упругого взаимодействия примеси с дислокацией от взаимодействия со сферическим геттером проявляется в том, что упругое поле последнего характеризуется чисто сдвиговой деформацией и энергия упругого взаимодействия равна нулю :
![]()
где К — модуль всестороннего сжатия материала среды, Wo — изменение объема, обусловленное примесным атомом, eii —дилатация упругого поля центра. Поэтому в условиях отсутствия ди-латацнонного взаимодействия и наличия пересыщения по собственным дефектам дальнодейст-вующий механизм упругого взаимодействия может быть реализован взаимодействием диполь-ного типа. Дипольные свойства примесного атома могут быть реализованы в случае образования комплекса из двух точечных дефектов: атом примеси—собственный точечный дефект или атом примеси—атом другой примеси.
Количественной мерой взаимодействия комплекса точечных дефектов с упругим полем центра дилатации является тетрагональность поля упругих искажений, создаваемых комплексом. В рамках континуальной теории упругости энергия точечного дефекта в поле eii задается выражением:
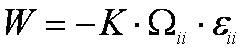
Тензор Wij, называемый тензором объемных деформаций, полностью характеризует упругие свойства точечного дефекта. Для упругого диполя с осевой симметрией он имеет вид :
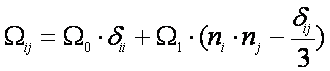
ni и nj — направляющие косинусы оси симметрии диполя.
Для последовательного .количественного описания образования примесных сегрегаций вблизи центра геттерирования необходимо знать параметры Wo и W1, характеризующие отдельный комплекс и определить распределение таких комплексов в пространстве, окружающем центр геттерирования. Расчеты характеристик комплекса проводились методом молекулярной статики. За основу был принят так называемый метод флекс-1 (метод гибкой границы с перекрывающимися областями). Кристалл разбивается на три области. Область 1, непосредственно окружающая кристалл, рассматривается как дискретная. В этой сильно искаженной области координаты атомов учитываются индивидуально, а энергия рассчитывается с помощью межатомного потенциала. Область 3, наиболее удаленная от дефекта, представляется как упругий континуум. Вклад этой области в общую энергию системы определяется решением уравнений теории упругости, т.е. величинами W0 и W1 и упругими постоянными среды. Область 2 является промежуточной. Координаты атомов в этой области определяются коллективно также » соответствии с теорией упругости, а вклад в энергию системы — с помощью межатомного потенциала. В ходе расчета минимизируется полная энергия системы, являющаяся функцией координат атомов и двух переменных Wo и W1, характеризующих дальнодействующее поле дефекта. Решение этой вариационной задачи и дает искомые величины.
